<ROUGH SET 러프 집합>
컴퓨터 과학에서 러프 집합은 Zdzisław I. Pawlak라는 폴란드의 컴퓨터 사이언티스트가 처음으로 제창했다. (81,2년인듯)
러프 집합은 전통적 집합이라고도 하는 crisp set의 정식 근사로 원래 집합의 하한, 상한 근사 두 가지 집합의 한 쌍이다. 1991년에 표준판의 rough set theory 러프 집합 이론은 하한과 상한 근사 집합이 crisp set이지만 다른 변수 하에서는 fuzzy set이 될 수도 있다. (대상 집합을 퍼지 집합으로 확장한 퍼지-러프 집합 이론도 있다고 하네 일본어판에는..)
crisp set ?
mathematical set. 우리가 흔히 아는 그런 집합을 의미 한다.
fuzzy set ?
각 element들의 membership의 degrees(소속도)를 가지고 있는... 집합.
이제 우리는 쥬지슬락 파블락이 처음에 제안한 러프셋 이론의 기본적인 프레임워크에 대해서 몇개 주요 정의를 놓고 알아볼 것이다. 더 포멀한 러프셋의 프로퍼티들과 바운더리들은 Pawlak(1991)에서 찾을 수 있고 레퍼런스에도 있다. 초기의 기본적인 러프셋의 이론은 "Pawlk Rough Set"이나 "Classical rough set"이라고도 하는데 최근의 확장되고 일반화 된 것들과 차별화 하기 위함이다.
Information System Framework 인포 시스템 프레임워크
다음과 같은 인포 시스템 프레임워크가 있다고 하자.
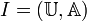
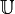 : universe, 유한한 공백 없는 집합
: universe, 유한한 공백 없는 집합
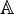 : 모든
: 모든  에 대해
에 대해  를 만족하는 공백없는 유한한 집합
를 만족하는 공백없는 유한한 집합
 : 속성
: 속성  가 가질 수 있는 값들의 집합
가 가질 수 있는 값들의 집합
이 인포 테이블은 전체집합 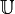 에서 각각의 속성
에서 각각의 속성  와 오브젝트
와 오브젝트  에 대해
에 대해  로부터
로부터 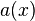 를 할당한다.
를 할당한다.
모든  에 대해 동등관계
에 대해 동등관계 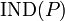 가 할당되는데
가 할당되는데
 로 표현 가능하다.
로 표현 가능하다.
관계 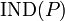 는
는  -indiscernibility relation P-식별불가능성 관계라고 불린다.
-indiscernibility relation P-식별불가능성 관계라고 불린다. 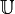 의 일부는 모든
의 일부는 모든 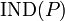 의 동등 클래스의 패밀리이며
의 동등 클래스의 패밀리이며  (or
(or  )로 나타낼 수 있다.
)로 나타낼 수 있다.
만약 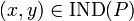 이면,
이면,  and
and  는
는  의 속성들로 "식별불가능"한 것이다.
의 속성들로 "식별불가능"한 것이다.
예 : 동등-클래스 구조
예를 들어 다음과 같은 인포 테이블을 보자.
| Object | 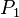 |  |  |  | 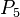 |
|---|---|---|---|---|---|
 | 1 | 2 | 0 | 1 | 1 |
 | 1 | 2 | 0 | 1 | 1 |
 | 2 | 0 | 0 | 1 | 0 |
 | 0 | 0 | 1 | 2 | 1 |
 | 2 | 1 | 0 | 2 | 1 |
 | 0 | 0 | 1 | 2 | 2 |
 | 2 | 0 | 0 | 1 | 0 |
 | 0 | 1 | 2 | 2 | 1 |
 | 2 | 1 | 0 | 2 | 2 |
 | 2 | 0 | 0 | 1 | 0 |
전체 속성 집합  를 생각해 볼 때, 우리는 다음과 같은 일곱개의 동등 클래스들이 있는걸 볼 수 있다 :
를 생각해 볼 때, 우리는 다음과 같은 일곱개의 동등 클래스들이 있는걸 볼 수 있다 :

첫번째 동등 클래스  는 나와있는 사용가능한 속성 값에 기초해서는 서로 구분 할 수가 없고, 두번째 동등 클래스인
는 나와있는 사용가능한 속성 값에 기초해서는 서로 구분 할 수가 없고, 두번째 동등 클래스인  도 서로를 구분할 수가 없다. 나머지 다섯개 오브젝트들은 서로서로 식별이 가능하다. P-식별불가능성 관계의 동등 클래스들은
도 서로를 구분할 수가 없다. 나머지 다섯개 오브젝트들은 서로서로 식별이 가능하다. P-식별불가능성 관계의 동등 클래스들은 ![[x]_P](http://upload.wikimedia.org/math/5/7/1/5716347ab104065a9ec16d77ec9c6b62.png) 로 나타낸다.
로 나타낸다.
속성의 다른 부분집합을 선택하면 보통 다른 식별불가능성 클래스들이 나올 것이라는 것은 명백하다. 예를 들면 속성값들 중에 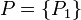 만 혼자 선택된다면, 우리는 다음과 같은 더욱 조잡한 동등 클래스 구조를 갖게 될 것이다 :
만 혼자 선택된다면, 우리는 다음과 같은 더욱 조잡한 동등 클래스 구조를 갖게 될 것이다 :
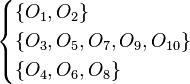
ROUGH SET의 정의 0.
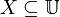 가 대상 집합이라고 하자. 우리는
가 대상 집합이라고 하자. 우리는  의 속성 부분집합을 사용하길 바란다. 즉, 우리는 오브젝트
의 속성 부분집합을 사용하길 바란다. 즉, 우리는 오브젝트  의 임의 집합(싱글 클래스를 포함하여)을 얘기하고자 하는 것이고, 속성 부분집합 P에 의해 유도된 동등 클래스를 사용하여 이 클래스(이 부분집합)을 표현하고자 하는 것이다. 보통,
의 임의 집합(싱글 클래스를 포함하여)을 얘기하고자 하는 것이고, 속성 부분집합 P에 의해 유도된 동등 클래스를 사용하여 이 클래스(이 부분집합)을 표현하고자 하는 것이다. 보통,  는 정확하게 표현 될 수 없다. 왜냐하면 집합은 속성
는 정확하게 표현 될 수 없다. 왜냐하면 집합은 속성  에 기초하여 구별할 수 없는 오브젝트들을 포함하거나 또는 포함하지 않을 수 있기 때문이다.
에 기초하여 구별할 수 없는 오브젝트들을 포함하거나 또는 포함하지 않을 수 있기 때문이다.
예를 들면, 대상집합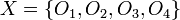 와 모든 가능한 피쳐들의 집합인 속성 부분집합
와 모든 가능한 피쳐들의 집합인 속성 부분집합  를 생각해보자.
를 생각해보자.
집합  는 정확히 표현될 수 없다는 것이 명시 될 것이다. 왜냐면
는 정확히 표현될 수 없다는 것이 명시 될 것이다. 왜냐면 ![[x]_P](http://upload.wikimedia.org/math/5/7/1/5716347ab104065a9ec16d77ec9c6b62.png) 에서, 오브젝트
에서, 오브젝트  들을 식별할 수 없기 때문이다. 그래서,
들을 식별할 수 없기 때문이다. 그래서,  and
and  을 제외하고
을 제외하고  만 포함하고 있는 집합
만 포함하고 있는 집합  를 표시할 방법이 없다. 그러나,
를 표시할 방법이 없다. 그러나,  의 근사치인
의 근사치인  -lower과
-lower과  -upper를 구축함으로써
-upper를 구축함으로써  안에 들어있는 정보만 가지고 대상 집합인
안에 들어있는 정보만 가지고 대상 집합인  를 대략 알 수 있다 :
를 대략 알 수 있다 :
1. Lower approximation and positive region 하한 근사와 포지티브 리전.. 명확한 영역- _-;;
 -하한 근사, 또는 Positive region은 대상 집합에 담겨진(부분집합인)
-하한 근사, 또는 Positive region은 대상 집합에 담겨진(부분집합인) ![[x]_P](http://upload.wikimedia.org/math/5/7/1/5716347ab104065a9ec16d77ec9c6b62.png) 의 모든 동등클래스들의 합이다. 예들들면, 대상 집합에 포함된
의 모든 동등클래스들의 합이다. 예들들면, 대상 집합에 포함된 ![[x]_P](http://upload.wikimedia.org/math/5/7/1/5716347ab104065a9ec16d77ec9c6b62.png) 의 두 동등집합의 합인
의 두 동등집합의 합인  . 하한 근사는 명확하게(모호하지 않게) 대상 집합
. 하한 근사는 명확하게(모호하지 않게) 대상 집합  로 분류될 수 있는
로 분류될 수 있는  의 오브젝트들의 완전집합이다. (완전집합 : 임의의 함수를 나타내기 위해 필요한 최소한의 속성 집합)
의 오브젝트들의 완전집합이다. (완전집합 : 임의의 함수를 나타내기 위해 필요한 최소한의 속성 집합)
2. Upper approximation and negative region 상한 근사와 네가티브 리전......... 하아.... 불확실한 영역.. ??
 -상한 근사는 대상 집합과 공백없는 교집합이 있는
-상한 근사는 대상 집합과 공백없는 교집합이 있는 ![[x]_P](http://upload.wikimedia.org/math/5/7/1/5716347ab104065a9ec16d77ec9c6b62.png) 의 모든 동등클래스의 합집합이다. 예를 들면, 대상 집합과 공백 없는 교집합을 가지고 있는
의 모든 동등클래스의 합집합이다. 예를 들면, 대상 집합과 공백 없는 교집합을 가지고 있는 ![[x]_P](http://upload.wikimedia.org/math/5/7/1/5716347ab104065a9ec16d77ec9c6b62.png) 의 세 동등 클래스들의 합집합인
의 세 동등 클래스들의 합집합인 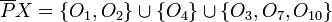 . 상한 근사는 대상 집합
. 상한 근사는 대상 집합  의 여집합(
의 여집합( )에 속하는지 명확하게(모호하지 않게) 분류될 수 없는
)에 속하는지 명확하게(모호하지 않게) 분류될 수 없는  안의 오브젝트들의 완전집합이다.
안의 오브젝트들의 완전집합이다.
 집합은 즉 네가티브 리전을 나타내는데, 확실히 대상 집합의 멤버로 제외될 수 있는 오브젝트들의 집합을 포함하고 있다.
집합은 즉 네가티브 리전을 나타내는데, 확실히 대상 집합의 멤버로 제외될 수 있는 오브젝트들의 집합을 포함하고 있다.
3. Boundary region 바운더리 리전
주어진 집합의 차  인 바운더리 리전은 대상 집합
인 바운더리 리전은 대상 집합  의 멤버로 포함되거나 또는 제외될 수 있는 오브젝트들로 구성되어있다.
의 멤버로 포함되거나 또는 제외될 수 있는 오브젝트들로 구성되어있다.
요약하자면, 대상 집합의 하한 근사는 집합의 멤버로 확실히 구별되어질 수 있는 오브젝트들 만으로 이루어진 conservative approximation 좀 소심하게 잡은 근사이다. (대상집합에서 제외된, 식별 불가능한 "클론"들이 없는 오브젝트들.) 상한 근사는 모든 대상 집합의 멤버가 될 수 있는 오브젝트들을 포함하는 liberal approximation 너그럽게 잡은 근사이다. (몇 상한 근사에 있는 오브젝트들은 대상 집합의 멤버가 아닐 수도 있다.)  의 관점에서, 하한 근사는 확실성이 있는(probability = 1) 대상집합의 멤버인 오브젝트들을 담고있고, 반면에 상한 근사는 0이 아닌 확률(probability > 0)의 대상 집합 멤버인 오브젝트를 담고 있다.
의 관점에서, 하한 근사는 확실성이 있는(probability = 1) 대상집합의 멤버인 오브젝트들을 담고있고, 반면에 상한 근사는 0이 아닌 확률(probability > 0)의 대상 집합 멤버인 오브젝트를 담고 있다.
4. The rough set 러프 집합
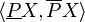 튜플은 러프 집합이라고 불리는 하한과 상한 근사로 구성되어있는데, 러프 집합은 두개의 보통 집합으로 이루어져있다. 하나는 대상 집합
튜플은 러프 집합이라고 불리는 하한과 상한 근사로 구성되어있는데, 러프 집합은 두개의 보통 집합으로 이루어져있다. 하나는 대상 집합  의 lower boundary를 나타내고, 다른 하나는 upper boundary를 나타낸다.
의 lower boundary를 나타내고, 다른 하나는 upper boundary를 나타낸다.
집합  를 나타내는 러프 집합의 accuracy는 다음과 같이 주어진다. (파블락이 91년에) :
를 나타내는 러프 집합의 accuracy는 다음과 같이 주어진다. (파블락이 91년에) :

즉,  를 나타내는 러프 집합의 정확도
를 나타내는 러프 집합의 정확도 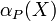 는
는  이고, 이것은
이고, 이것은  에 확실히 positively 들어갈 수 있는 오브젝트들의 숫자와 아마도 들어갈 수 있는 possibly 오브젝트들의 숫자의 비율이다ㅡ 이것은 러프 집합이 얼마나 대상 집합의 근사를 측정할 수 있는지를 제공해 준다. 명확하게, 상한과 하한근사가 같을 때(즉, 바운더리 리전이 공집합일 때),
에 확실히 positively 들어갈 수 있는 오브젝트들의 숫자와 아마도 들어갈 수 있는 possibly 오브젝트들의 숫자의 비율이다ㅡ 이것은 러프 집합이 얼마나 대상 집합의 근사를 측정할 수 있는지를 제공해 준다. 명확하게, 상한과 하한근사가 같을 때(즉, 바운더리 리전이 공집합일 때),  이고, 근사는 완벽하다. 반대로, 하한 근사가 공집합일 때는 언제나 정확도는 제로이다 (상한 근사 값의 크기에는 상관없이).
이고, 근사는 완벽하다. 반대로, 하한 근사가 공집합일 때는 언제나 정확도는 제로이다 (상한 근사 값의 크기에는 상관없이).
5. Objective analysis
러프 집합 이론은 불특정한(아주 쪼금인 것을 포함) 시스템에 적용할 수 있는 많은 방법들 중 하나이다. 다른 좀 더 전통적인 방법들인 확률과 통계, 엔트로피, Dempster-Shafer 이론보다 많이 쓰이지는 않지만 이들과의 핵심적인 차이와 고전적인 러프 집합 이론을 사용하는 것의 유니크한 강점은, 분석의 객관적인 형태를 제공해 준다는 것이다(파블락이 95년에 그랬음). 다른 방법들과는 다르게, 위에 주어져 있듯이, 고전적인 러프 집합 분석은 추가적인 정보가 필요없고, 외부 파라미터나 모델, 함수, 그레이드, 집합의 멤버십을 결정하기 위한 주관적인 해석 또한 필요없다. 오로지 주어진 데이터들에 나와있는 정보 사용한다. 더 최근에 러프 집합 이론이 적용된 dominance-based, dicision-theoretic, fuzzy rough set 같은 것들은 분석에 주관을 더 준 것이다.
Definability
보통, 상한/하한 근사는 같지 않다. 이런 경우에 우리는 대상집합  가 속성집합
가 속성집합  에 대해 undefinable하다고 하거나 roughly definable하다고 한다. 상한과 하한 근사가 같을 때,(즉, 바운더리가 공집합일 때,)
에 대해 undefinable하다고 하거나 roughly definable하다고 한다. 상한과 하한 근사가 같을 때,(즉, 바운더리가 공집합일 때,)  이다. 그러면 대상 집합
이다. 그러면 대상 집합  는 속성 집합
는 속성 집합  에 대해 definable하다고 한다. 우리는 다음과 같은 undefinability의 특별한 경우들을 구별 할 수 있다 :
에 대해 definable하다고 한다. 우리는 다음과 같은 undefinability의 특별한 경우들을 구별 할 수 있다 :
- 집합  는
는  and
and  일 때 내부적으로 정의불가능 이다. 이것은 속성 집합
일 때 내부적으로 정의불가능 이다. 이것은 속성 집합  에, 대상 집합
에, 대상 집합  에 확실히 속한 오브젝트들이 있지만, 집합
에 확실히 속한 오브젝트들이 있지만, 집합  에서 확실히 제외할 수 있는 오브젝트는 없다는 뜻이다.
에서 확실히 제외할 수 있는 오브젝트는 없다는 뜻이다.
- 집합  는
는  and
and 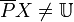 일 때 외부적으로 정의불가능 이다. 이것은 속성 집합
일 때 외부적으로 정의불가능 이다. 이것은 속성 집합  에, 대상 집합
에, 대상 집합  에 확실히 속한 오브젝트들은 없지만, 집합
에 확실히 속한 오브젝트들은 없지만, 집합  에서 확실히 제외할 수 있는 오브젝트는 있다는 뜻이다.
에서 확실히 제외할 수 있는 오브젝트는 있다는 뜻이다.
- 집합  는
는  and
and  일 때 완전히 정의 불가능 이다. 이것은 속성집합
일 때 완전히 정의 불가능 이다. 이것은 속성집합  에, 대상 집합
에, 대상 집합  에 확실히 속한 오브젝트들이 없고, 집합
에 확실히 속한 오브젝트들이 없고, 집합  에서 확실히 제외할 수 있는 오브젝트도 없다는 뜻이다. 그러므로 속성집합
에서 확실히 제외할 수 있는 오브젝트도 없다는 뜻이다. 그러므로 속성집합  에서 우리는 어떤 오브젝트도
에서 우리는 어떤 오브젝트도  의 멤버인지 아닌지 결정 할 수가 없다.
의 멤버인지 아닌지 결정 할 수가 없다.
Reduct and core
흥미로운 질문 하나는, 다른 속성들 보다 더 동등클래스 구조에서 knowledge에 중요하게 나타나는 속성이 인포 시스템(속성-값 테이블)에 있느냐는 것이다.
Reduct라는 속성 집합 : 스스로 데이터베이스의 knowledge를 전부 특성화 할 수 있는 속성들의 부분집합.
정식적으로, 리덕트는 속성들의 부분집합 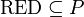 인데 이것은
인데 이것은
- ![[x]_{\mathrm{RED}}](http://upload.wikimedia.org/math/7/3/e/73eaf34c3ce3fa25f830b13b74825f93.png) =
= ![[x]_P](http://upload.wikimedia.org/math/5/7/1/5716347ab104065a9ec16d77ec9c6b62.png) 이다. 즉, 줄어든 속성 집합
이다. 즉, 줄어든 속성 집합  에 의해 유도된 동등 클래스들은 전체 속성 집합
에 의해 유도된 동등 클래스들은 전체 속성 집합  에 의해 유도된 동등 클래스 구조와 같다.
에 의해 유도된 동등 클래스 구조와 같다.
- 속성 집합  는 최소형태이다. 모든 속성
는 최소형태이다. 모든 속성  에 대해
에 대해 ![[x]_{(\mathrm{RED}-\{a\})} \neq [x]_P](http://upload.wikimedia.org/math/2/d/f/2dfaba469477c41fa58ad8eab9b45308.png) 라는 의미에서. 즉,
라는 의미에서. 즉,  집합에서 동등 클래스
집합에서 동등 클래스 ![[x]_P](http://upload.wikimedia.org/math/5/7/1/5716347ab104065a9ec16d77ec9c6b62.png) 를 바꾸지 않고서는 그 어떤 속성도 없앨 수 없다.
를 바꾸지 않고서는 그 어떤 속성도 없앨 수 없다.
리덕트는 피쳐들의 sufficient 집합이라고 생각될 수 있다. 즉, 카테고리 구조를 대표하기에 충분하다는 것이다. 위의 예시 테이블에서, 속성 집합  는 리덕트이다. 인포 시스템이 이 속성들로 프로젝트 되면 전체 속성 집합에 의해 표현되는 동등클래스 구조와 같은 것을 갖게 된다.
는 리덕트이다. 인포 시스템이 이 속성들로 프로젝트 되면 전체 속성 집합에 의해 표현되는 동등클래스 구조와 같은 것을 갖게 된다.

속성 집합  는 적합한 리덕트 이다 왜냐하면 이 중에 어떤 속성이라도 제거하게 되면
는 적합한 리덕트 이다 왜냐하면 이 중에 어떤 속성이라도 제거하게 되면 ![[x]_{\mathrm{RED}} \neq [x]_P](http://upload.wikimedia.org/math/7/9/7/797eda0d5d141d7dc7e086d3f29caae2.png) 가 되어 동등 클래스 구조가 무너지기 때문이다.
가 되어 동등 클래스 구조가 무너지기 때문이다.
인포시스템의 리덕트는 유일한 것이 아니다. 동등 클래스 구조(knowledge)를 유지하는 많은 서로 다른 부분 집합들이 존재할 수 있다. 위의 예시 인포 시스템에서,  리덕트도 똑같은 동등 클래스 구조를 가진다.
리덕트도 똑같은 동등 클래스 구조를 가진다.
Core : 모든 리덕트들에 공통적으로 있는 속성들의 집합.
코어는 모든 적합한 리덕트들이 가지고 있는 속성들의 집합이다. 그러므로 동등 클래스 구조를 바꾸지 않고는 인포 시스템에서 제거될 수 없는 속성들로 이루어져 있다.
코어는 필수 속성들이라고 생각되어질 수도 있다. 필수적이라는 것은 카테고리 구조를 대표할 수 있다는 것이다.
위의 예에서 그러한 속성은  뿐이다. 다른 속성들은 모두 개별적으로 동등 클래스 구조에 변화 없이 제거 될 수 있다 그리고 그러한 것들은 모두 dispensable하다고 한다. 그러나
뿐이다. 다른 속성들은 모두 개별적으로 동등 클래스 구조에 변화 없이 제거 될 수 있다 그리고 그러한 것들은 모두 dispensable하다고 한다. 그러나  없애면 동등 클래스 구조를 바꾼다. 그러므로 이것은 이 인포 시스템에서 indispensable한 것이다. 그리고 코어라고 한다.
없애면 동등 클래스 구조를 바꾼다. 그러므로 이것은 이 인포 시스템에서 indispensable한 것이다. 그리고 코어라고 한다.
코어는 아예 없을 수도 있다. indispensable한 속성이 없다는 뜻이다. 모든 속성들이 동등 클래스 구조를 바꾸지 않고 제거 될 수 있다. 이러한 경우에, essential 또는 necessary 속성이 없다고 한다.
'춤추는 프로그래머 > Machine Learning.' 카테고리의 다른 글
| 공부 할 것 (0) | 2014.07.16 |
|---|---|
| 이태리논문 ) Entity Linking의 learning relatedness 측정 요약 (1) | 2014.02.02 |
| Entity Linking system (0) | 2014.01.21 |
| Entity Linking (from wiki) (0) | 2014.01.21 |
| 유한상태기계(Finite State Machine, FSM) 이란? (0) | 2013.04.10 |
![{\underline P}X= \{x \mid [x]_P \subseteq X\}](http://upload.wikimedia.org/math/e/4/f/e4f4ec93ab81c92a337b3aa636e65e54.png)
![{\overline P}X = \{x \mid [x]_P \cap X \neq \emptyset \}](http://upload.wikimedia.org/math/b/8/8/b88264ed716b07d8885f3ddef897e54a.png)